21. Dropout Neural Networks in Python
By Bernd Klein. Last modified: 19 Apr 2024.
Introduction
The term "dropout" is used for a technique which drops out some nodes of the network. Dropping out can be seen as temporarily deactivating or ignoring neurons of the network. This technique is applied in the training phase to reduce overfitting effects. Overfitting is an error which occurs when a network is too closely fit to a limited set of input samples.
The basic idea behind dropout neural networks is to dropout nodes so that the network can concentrate on other features. Think about it like this. You watch lots of films from your favourite actor. At some point you listen to the radio and here somebody in an interview. You don't recognize your favourite actor, because you have seen only movies and your are a visual type. Now, imagine that you can only listen to the audio tracks of the films. In this case you will have to learn to differentiate the voices of the actresses and actors. So by dropping out the visual part you are forced tp focus on the sound features!
This technique has been first proposed in a paper "Dropout: A Simple Way to Prevent Neural Networks from Overfitting" by Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever and Ruslan Salakhutdinov in 2014
We will implement in our tutorial on machine learning in Python a Python class which is capable of dropout.
Live Python training
See our Python training courses
Modifying the Weight Arrays
If we deactivate a node, we have to modify the weight arrays accordingly. To demonstrate how this can be accomplished, we will use a network with three input nodes, four hidden and two output nodes:
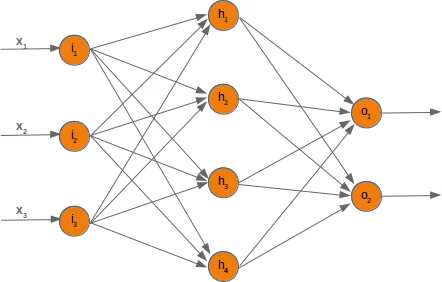
At first, we will have a look at the weight array between the input and the hidden layer. We called this array 'wih' (weights between input and hidden layer).
Let's deactivate (drop out) the node $i_2$. We can see in the following diagram what's happening:

This means that we have to take out every second product of the summation, which means that we have to delete the whole second column of the matrix. The second element from the input vector has to be deleted as well.
Now we will examine what happens if we take out a hidden node. We take out the first hidden node, i.e. $h_1$.

In this case, we can remove the complete first line of our weight matrix:
Taking out a hidden node affects the next weight matrix as well. Let's have a look at what is happening in the network graph:
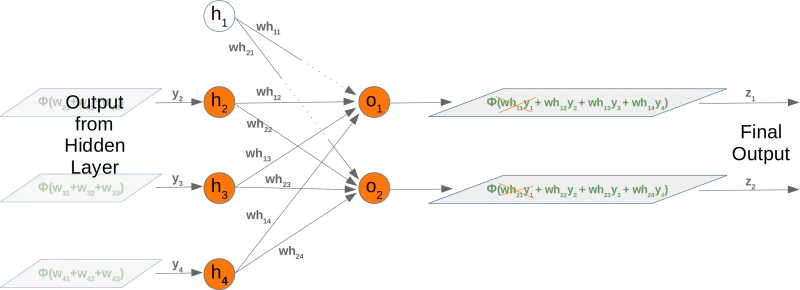
It is easy to see that the first column of the who weight matrix has to be removed again:
So far we have arbitrarily chosen one node to deactivate. The dropout approach means that we randomly choose a certain number of nodes from the input and the hidden layers, which remain active and turn off the other nodes of these layers. After this we can train a part of our learn set with this network. The next step consists in activating all the nodes again and randomly chose other nodes. It is also possible to train the whole training set with the randomly created dropout networks.
We present three possible randomly chosen dropout networks in the following three diagrams:
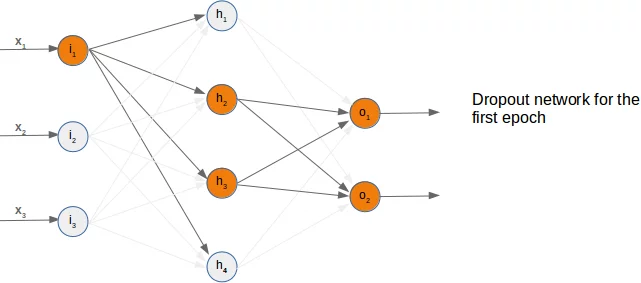
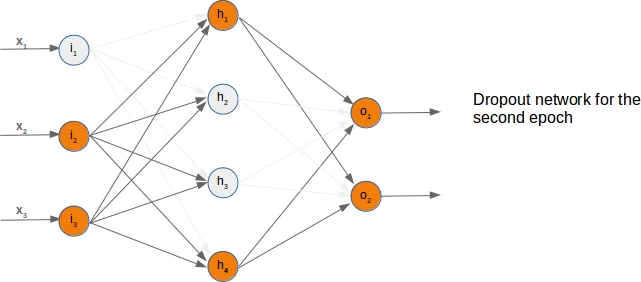
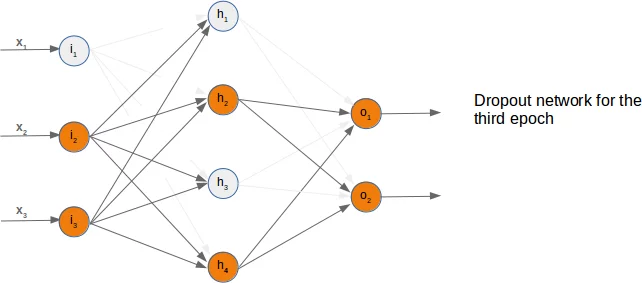
Now it is time to think about a possible Python implementation.
We will start with the weight matrix between input and hidden layer. We will randomly create a weight matrix for 10 input nodes and 5 hidden nodes. We fill our matrix with random numbers between -10 and 10, which are not proper weight values, but this way we can see better what is going on:
import numpy as np
import random
input_nodes = 10
hidden_nodes = 5
output_nodes = 7
wih = np.random.randint(-10, 10, (hidden_nodes, input_nodes))
wih
OUTPUT:
array([[ -8, 8, -4, -7, 5, -7, -9, 6, -4, -10],
[ -2, 1, -3, -9, 3, 8, 1, 1, -3, 5],
[-10, -5, -5, 8, -4, 7, 4, 4, 0, 0],
[ 6, -3, -3, 1, -1, -6, 8, -7, 2, -8],
[ -6, 7, 4, 6, -2, 3, 3, -8, 6, 3]])
We will choose now the active nodes for the input layer. We calculate random indices for the active nodes:
active_input_percentage = 0.7
active_input_nodes = int(input_nodes * active_input_percentage)
active_input_indices = sorted(random.sample(range(0, input_nodes),
active_input_nodes))
active_input_indices
OUTPUT:
[0, 1, 4, 5, 6, 8, 9]
We learned above that we have to remove the column $j$, if the node $i_j$ is removed. We can easily accomplish this for all deactived nodes by using the slicing operator with the active nodes:
wih_old = wih.copy()
wih = wih[:, active_input_indices]
wih
OUTPUT:
array([[ -8, 8, 5, -7, -9, -4, -10],
[ -2, 1, 3, 8, 1, -3, 5],
[-10, -5, -4, 7, 4, 0, 0],
[ 6, -3, -1, -6, 8, 2, -8],
[ -6, 7, -2, 3, 3, 6, 3]])
As we have mentioned before, we will have to modify both the 'wih' and the 'who' matrix:
who = np.random.randint(-10, 10, (output_nodes, hidden_nodes))
print(who)
active_hidden_percentage = 0.7
active_hidden_nodes = int(hidden_nodes * active_hidden_percentage)
active_hidden_indices = sorted(random.sample(range(0, hidden_nodes),
active_hidden_nodes))
print(active_hidden_indices)
who_old = who.copy()
who = who[:, active_hidden_indices]
print(who)
OUTPUT:
[[ -4 -9 -7 -10 -9] [ -3 5 -1 -10 -2] [ 1 0 0 -1 6] [ 4 3 -7 -9 7] [ -8 -3 5 8 0] [ -7 5 -3 -1 9] [ 4 -5 -1 9 4]] [0, 1, 3] [[ -4 -9 -10] [ -3 5 -10] [ 1 0 -1] [ 4 3 -9] [ -8 -3 8] [ -7 5 -1] [ 4 -5 9]]
We have to change wih accordingly:
wih = wih[active_hidden_indices]
wih
OUTPUT:
array([[ -8, 8, 5, -7, -9, -4, -10],
[ -2, 1, 3, 8, 1, -3, 5],
[ 6, -3, -1, -6, 8, 2, -8]])
The following Python code summarizes the sniplets from above:
import numpy as np
import random
input_nodes = 10
hidden_nodes = 5
output_nodes = 7
wih = np.random.randint(-10, 10, (hidden_nodes, input_nodes))
print("wih: \n", wih)
who = np.random.randint(-10, 10, (output_nodes, hidden_nodes))
print("who:\n", who)
active_input_percentage = 0.7
active_hidden_percentage = 0.7
active_input_nodes = int(input_nodes * active_input_percentage)
active_input_indices = sorted(random.sample(range(0, input_nodes),
active_input_nodes))
print("\nactive input indices: ", active_input_indices)
active_hidden_nodes = int(hidden_nodes * active_hidden_percentage)
active_hidden_indices = sorted(random.sample(range(0, hidden_nodes),
active_hidden_nodes))
print("active hidden indices: ", active_hidden_indices)
wih_old = wih.copy()
wih = wih[:, active_input_indices]
print("\nwih after deactivating input nodes:\n", wih)
wih = wih[active_hidden_indices]
print("\nwih after deactivating hidden nodes:\n", wih)
who_old = who.copy()
who = who[:, active_hidden_indices]
print("\nwih after deactivating hidden nodes:\n", who)
OUTPUT:
wih: [[ 5 -2 0 9 6 -9 -3 -8 -8 -4] [ 9 -6 -7 -9 -7 0 -7 -5 5 -5] [ -1 1 6 9 -8 -2 -8 -6 -8 -9] [ 9 6 4 -2 -8 7 8 -9 -10 9] [ -9 4 -6 -9 8 4 6 0 -3 4]] who: [[ 4 -10 -10 1 6] [ -3 8 9 -7 3] [ 3 -7 8 -8 -4] [ 4 9 -3 -3 4] [ 7 7 -4 7 -9] [ -1 3 -2 5 -4] [ -2 -9 9 9 -6]] active input indices: [0, 1, 2, 3, 4, 5, 9] active hidden indices: [0, 1, 3] wih after deactivating input nodes: [[ 5 -2 0 9 6 -9 -4] [ 9 -6 -7 -9 -7 0 -5] [-1 1 6 9 -8 -2 -9] [ 9 6 4 -2 -8 7 9] [-9 4 -6 -9 8 4 4]] wih after deactivating hidden nodes: [[ 5 -2 0 9 6 -9 -4] [ 9 -6 -7 -9 -7 0 -5] [ 9 6 4 -2 -8 7 9]] wih after deactivating hidden nodes: [[ 4 -10 1] [ -3 8 -7] [ 3 -7 -8] [ 4 9 -3] [ 7 7 7] [ -1 3 5] [ -2 -9 9]]
import numpy as np
import random
from scipy.special import expit as activation_function
from scipy.stats import truncnorm
def truncated_normal(mean=0, sd=1, low=0, upp=10):
return truncnorm(
(low - mean) / sd, (upp - mean) / sd, loc=mean, scale=sd)
class NeuralNetwork:
def __init__(self,
no_of_in_nodes,
no_of_out_nodes,
no_of_hidden_nodes,
learning_rate,
bias=None
):
self.no_of_in_nodes = no_of_in_nodes
self.no_of_out_nodes = no_of_out_nodes
self.no_of_hidden_nodes = no_of_hidden_nodes
self.learning_rate = learning_rate
self.bias = bias
self.create_weight_matrices()
def create_weight_matrices(self):
X = truncated_normal(mean=2, sd=1, low=-0.5, upp=0.5)
bias_node = 1 if self.bias else 0
n = (self.no_of_in_nodes + bias_node) * self.no_of_hidden_nodes
X = truncated_normal(mean=2, sd=1, low=-0.5, upp=0.5)
self.wih = X.rvs(n).reshape((self.no_of_hidden_nodes,
self.no_of_in_nodes + bias_node))
n = (self.no_of_hidden_nodes + bias_node) * self.no_of_out_nodes
X = truncated_normal(mean=2, sd=1, low=-0.5, upp=0.5)
self.who = X.rvs(n).reshape((self.no_of_out_nodes,
(self.no_of_hidden_nodes + bias_node)))
def dropout_weight_matrices(self,
active_input_percentage=0.70,
active_hidden_percentage=0.70):
# restore wih array, if it had been used for dropout
self.wih_orig = self.wih.copy()
self.no_of_in_nodes_orig = self.no_of_in_nodes
self.no_of_hidden_nodes_orig = self.no_of_hidden_nodes
self.who_orig = self.who.copy()
active_input_nodes = int(self.no_of_in_nodes * active_input_percentage)
active_input_indices = sorted(random.sample(range(0, self.no_of_in_nodes),
active_input_nodes))
active_hidden_nodes = int(self.no_of_hidden_nodes * active_hidden_percentage)
active_hidden_indices = sorted(random.sample(range(0, self.no_of_hidden_nodes),
active_hidden_nodes))
self.wih = self.wih[:, active_input_indices][active_hidden_indices]
self.who = self.who[:, active_hidden_indices]
self.no_of_hidden_nodes = active_hidden_nodes
self.no_of_in_nodes = active_input_nodes
return active_input_indices, active_hidden_indices
def weight_matrices_reset(self,
active_input_indices,
active_hidden_indices):
"""
self.wih and self.who contain the newly adapted values from the active nodes.
We have to reconstruct the original weight matrices by assigning the new values
from the active nodes
"""
temp = self.wih_orig.copy()[:,active_input_indices]
temp[active_hidden_indices] = self.wih
self.wih_orig[:, active_input_indices] = temp
self.wih = self.wih_orig.copy()
self.who_orig[:, active_hidden_indices] = self.who
self.who = self.who_orig.copy()
self.no_of_in_nodes = self.no_of_in_nodes_orig
self.no_of_hidden_nodes = self.no_of_hidden_nodes_orig
def train_single(self, input_vector, target_vector):
"""
input_vector and target_vector can be tuple, list or ndarray
"""
if self.bias:
# adding bias node to the end of the input_vector
input_vector = np.concatenate( (input_vector, [self.bias]) )
input_vector = np.array(input_vector, ndmin=2).T
target_vector = np.array(target_vector, ndmin=2).T
output_vector1 = np.dot(self.wih, input_vector)
output_vector_hidden = activation_function(output_vector1)
if self.bias:
output_vector_hidden = np.concatenate( (output_vector_hidden, [[self.bias]]) )
output_vector2 = np.dot(self.who, output_vector_hidden)
output_vector_network = activation_function(output_vector2)
output_errors = target_vector - output_vector_network
# update the weights:
tmp = output_errors * output_vector_network * (1.0 - output_vector_network)
tmp = self.learning_rate * np.dot(tmp, output_vector_hidden.T)
self.who += tmp
# calculate hidden errors:
hidden_errors = np.dot(self.who.T, output_errors)
# update the weights:
tmp = hidden_errors * output_vector_hidden * (1.0 - output_vector_hidden)
if self.bias:
x = np.dot(tmp, input_vector.T)[:-1,:]
else:
x = np.dot(tmp, input_vector.T)
self.wih += self.learning_rate * x
def train(self, data_array,
labels_one_hot_array,
epochs=1,
active_input_percentage=0.70,
active_hidden_percentage=0.70,
no_of_dropout_tests = 10):
partition_length = int(len(data_array) / no_of_dropout_tests)
for epoch in range(epochs):
print("epoch: ", epoch)
for start in range(0, len(data_array), partition_length):
active_in_indices, active_hidden_indices = \
self.dropout_weight_matrices(active_input_percentage,
active_hidden_percentage)
for i in range(start, start + partition_length):
self.train_single(data_array[i][active_in_indices],
labels_one_hot_array[i])
self.weight_matrices_reset(active_in_indices, active_hidden_indices)
def confusion_matrix(self, data_array, labels):
cm = {}
for i in range(len(data_array)):
res = self.run(data_array[i])
res_max = res.argmax()
target = labels[i][0]
if (target, res_max) in cm:
cm[(target, res_max)] += 1
else:
cm[(target, res_max)] = 1
return cm
def run(self, input_vector):
# input_vector can be tuple, list or ndarray
if self.bias:
# adding bias node to the end of the input_vector
input_vector = np.concatenate( (input_vector, [self.bias]) )
input_vector = np.array(input_vector, ndmin=2).T
output_vector = np.dot(self.wih, input_vector)
output_vector = activation_function(output_vector)
if self.bias:
output_vector = np.concatenate( (output_vector, [[self.bias]]) )
output_vector = np.dot(self.who, output_vector)
output_vector = activation_function(output_vector)
return output_vector
def evaluate(self, data, labels):
corrects, wrongs = 0, 0
for i in range(len(data)):
res = self.run(data[i])
res_max = res.argmax()
if res_max == labels[i]:
corrects += 1
else:
wrongs += 1
return corrects, wrongs
import pickle
with open("../data/mnist/pickled_mnist.pkl", "br") as fh:
data = pickle.load(fh)
train_imgs = data[0]
test_imgs = data[1]
train_labels = data[2]
test_labels = data[3]
digits = np.arange(10)
train_labels_one_hot = (digits==train_labels).astype(np.float64)
test_labels_one_hot = (digits==test_labels).astype(np.float64)
image_size = 28 # width and length
no_of_different_labels = 10 # i.e. 0, 1, 2, 3, ..., 9
image_pixels = image_size * image_size
parts = 10
partition_length = int(len(train_imgs) / parts)
print(partition_length)
start = 0
for start in range(0, len(train_imgs), partition_length):
print(start, start + partition_length)
OUTPUT:
6000 0 6000 6000 12000 12000 18000 18000 24000 24000 30000 30000 36000 36000 42000 42000 48000 48000 54000 54000 60000
epochs = 3
simple_network = NeuralNetwork(no_of_in_nodes = image_pixels,
no_of_out_nodes = 10,
no_of_hidden_nodes = 100,
learning_rate = 0.1)
simple_network.train(train_imgs,
train_labels_one_hot,
active_input_percentage=1,
active_hidden_percentage=1,
no_of_dropout_tests = 100,
epochs=epochs)
OUTPUT:
epoch: 0 epoch: 1 epoch: 2
corrects, wrongs = simple_network.evaluate(train_imgs, train_labels)
print("accuracy train: ", corrects / ( corrects + wrongs))
corrects, wrongs = simple_network.evaluate(test_imgs, test_labels)
print("accuracy: test", corrects / ( corrects + wrongs))
OUTPUT:
accuracy train: 0.9198666666666667 accuracy: test 0.9226
