10. Neural Networks Introduction
By Bernd Klein. Last modified: 17 Feb 2022.
Introduction
When we say "Neural Networks", we mean artificial Neural Networks (ANN). The idea of ANN is based on biological neural networks like the brain of living being.
The basic structure of a neural network - both an artificial and a living one - is the neuron. A neuron in biology consists of three major parts: the soma (cell body), the dendrites and the axon.
The dendrites branch of from the soma in a tree-like way and become thinner with every branch. They receive signals (impulses) from other neurons at synapses. The axon - there is always only one - also leaves the soma and usually tend to extend for longer distances than the dentrites. The axon is used for sending the output of the neuron to other neurons or better to the synapsis of other neurons.
Live Python training
See our Python training courses
Biological Neuron
The following image by Quasar Jarosz, courtesy of Wikipedia, illustrates this:
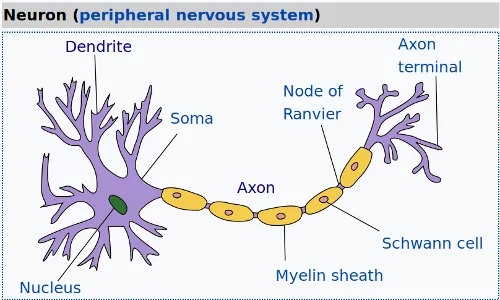
Abstraction of a Biological Neuron and Artificial Neuron
Even though the above image is already an abstraction for a biologist, we can further abstract it:
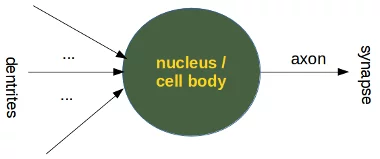
A perceptron of artificial neural networks is simulating a biological neuron.
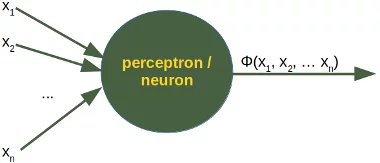
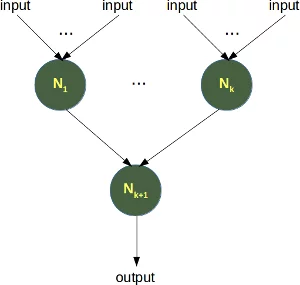
It is amazingly simple, what is going on inside the body of a perceptron or neuron. The input signals get multiplied by weight values, i.e. each input has its corresponding weight. This way the input can be adjusted individually for every $x_i$. We can see all the inputs as an input vector and the corresponding weights as the weights vector.
When a signal comes in, it gets multiplied by a weight value that is assigned to this particular input. That is, if a neuron has three inputs, then it has three weights that can be adjusted individually. The weights usually get adjusted during the learn phase.
After this the modified input signals are summed up. It is also possible to add additionally a so-called bias 'b' to this sum. The bias is a value which can also be adjusted during the learn phase.
Finally, the actual output has to be determined. For this purpose an activation or step function Φ is applied to the weighted sum of the input values.
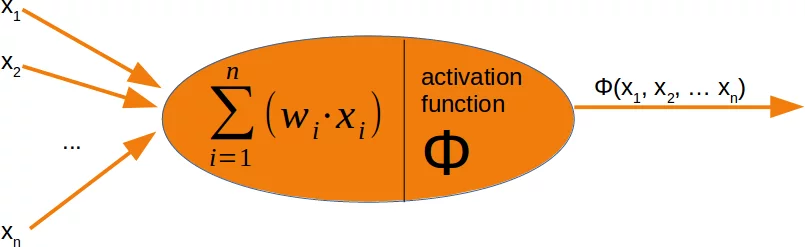
The simplest form of an activation function is a binary function. If the result of the summation is greater than some threshold s, the result of $\Phi$ will be 1, otherwise 0.
$$ \Phi(x) = \left\{ \begin{array}{rl} 1 &\mbox{ wx + b > s} \\ 0 &\mbox{ otherwise} \end{array} \right.$$
Number of Neuron in Animals
We will examine in the following chapters artificial neuronal networks of various sizes and structures. It is interesting to have a look at the total numbers of neurons some animals have:
| Animal | Nervous System | Brain |
|---|---|---|
| Roundworm | 302 | |
| Jellyfish | 5600 | |
| Lobster | 100000 | |
| Ant | 250000 | |
| Honey bee | 960000 | |
| Frog | 16,000,000 | |
| House Mouse | 71,000,000 | 4,000,000 |
| Rabit | 494,000,000 | 71,450,000 |
| Octopus | 500,000,000 | 25,000,000 |
| Cat | 760,000,000 | 250,000,000 |
| Dog | 2,253,000,000 | 530,000,000 |
| Lion | 4,910,000,000 | 545,000,000 |
| Orangutan | 32,600,000,000 | 8,900,000,000 |
| Gorilla | 33,400,000,000 | 9,100,000,000 |
| Human | 86,000,000,000 | 16,000,000,000 |
| Long-finned pilot whale | 37,200,000,000 |
