10. Matrix Arithmetics under NumPy and Python
By Bernd Klein. Last modified: 24 Mar 2022.
In the previous chapter of our introduction in NumPy we have demonstrated how to create and change Arrays. In this chapter we want to show, how we can perform in Python with the module NumPy all the basic Matrix Arithmetics like
- Matrix addition
- Matrix subtraction
- Matrix multiplication
- Scalar product
- Cross product
- and lots of other operations on matrices
The arithemtic standard Operators
- +
- -
- *
- /
- %
are applied on the elements, this means that the arrays have to have the same size.
import numpy as np
x = np.array([1, 5, 2])
y = np.array([7, 4, 1])
x + y
OUTPUT:
array([8, 9, 3])
x * y
OUTPUT:
array([ 7, 20, 2])
x - y
OUTPUT:
array([-6, 1, 1])
x / y
OUTPUT:
array([0.14285714, 1.25 , 2. ])
x % y
OUTPUT:
array([1, 1, 0])
Vector Addition and Subtraction
Many people know vector addition and subtraction from physics, to be exact from the parallelogram of forces. It is a method for solving (or visualizing) the results of applying two forces to an object.
The addition of two vectors, in our example (see picture) x and y, may be represented graphically by placing the start of the arrow y at the tip of the arrow x, and then drawing an arrow from the start (tail) of x to the tip (head) of y. The new arrow drawn represents the vector x + y
x = np.array([3, 2])
y = np.array([5, 1])
z = x + y
z
OUTPUT:
array([8, 3])
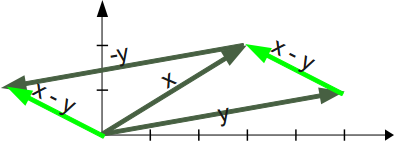
Subtracting a vector is the same as adding its negative. So, the difference of the vectors x and y is equal to the sum of x and -y: x - y = x + (-y) Subtraction of two vectors can be geometrically defined as follows: to subtract y from x, we place the end points of x and y at the same point, and then draw an arrow from the tip of y to the tip of x. That arrow represents the vector x - y, see picture on the right side.
Mathematically, we subtract the corresponding components of vector y from the vector x.
Live Python training
See our Python training courses
Scalar Product / Dot Product

In mathematics, the dot product is an algebraic operation that takes two coordinate vectors of equal size and returns a single number. The result is calculated by multiplying corresponding entries and adding up those products. The name "dot product" stems from the fact that the centered dot "·" is often used to designate this operation. The name "scalar product" focusses on the scalar nature of the result. of the result.
Definition of the scalar product:
![]()
We can see from the definition of the scalar product that it can be used to calculate the cosine of the angle between two vectors.
Calculation of the scalar product:
![]()
Finally, we want to demonstrate how to calculate the scalar product in Python:
x = np.array([1, 2, 3])
y = np.array([-7, 8, 9])
np.dot(x, y)
OUTPUT:
36
dot = np.dot(x ,y)
x_modulus = np.sqrt((x*x).sum())
y_modulus = np.sqrt((y*y).sum())
cos_angle = dot / x_modulus / y_modulus # cosine of angle between x and y
angle = np.arccos(cos_angle)
angle
OUTPUT:
0.808233789010825
angle * 360 / 2 / np.pi # angle in degrees
OUTPUT:
46.308384970187326
36
>>> dot = np.dot(x,y)
>>> x_modulus = np.sqrt((x*x).sum())
>>> y_modulus = np.sqrt((y*y).sum())
>>> cos_angle = dot / x_modulus / y_modulus # cosine of angle between x and y
>>> angle = np.arccos(cos_angle)
>>> angle
0.80823378901082499
>>> angle * 360 / 2 / np.pi # angle in degrees
OUTPUT:
46.308384970187326
Matrix Product
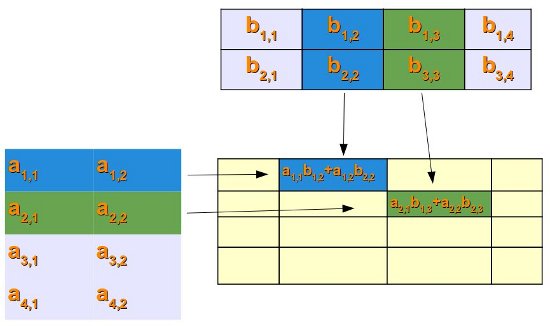
The matrix product of two matrices can be calculated if the number of columns of the left matrix is equal to the number of rows of the second or right matrix.
The product of a (l x m)-matrix A = (aij)i=1...l, j= 1..m and an (m x n)-matrix B = (bij)i=1...m, j= 1..n is a matrix C = (cij)i=1...l, j= 1..n, which is calculated like this:
![]()
The following picture illustrates it further:
If we want to perform matrix multiplication with two numpy arrays (ndarray), we have to use the dot product:
x = np.array( ((2,3), (3, 5)) )
y = np.matrix( ((1,2), (5, -1)) )
print(np.dot(x,y))
OUTPUT:
[[17 1] [28 1]]
Simple Practical Application for Matrix Multiplication

In the following practical example, we come to talk about the sweet things of life.
Let's assume there are four people, and we call them Lucas, Mia, Leon and Hannah. Each of them has bought chocolates out of a choice of three. The brand are A, B and C, not very marketable, we have to admit. Lucas bought 100 g of brand A, 175 g of brand B and 210 of C. Mia choose 90 g of A, 160 g of B and 150 g of C. Leon bought 200 g of A, 50 of B and 100 g of C. Hannah apparently didn't like brand B, because she hadn't bought any of those. But she she seems to be a real fan of brand C, because she bought 310 g of them. Furthermore she bought 120 g of A.
So, what's the price in Euro of these chocolates: A costs 2.98 per 100 g, B costs 3.90 and C only 1.99 Euro.
If we have to calculate how much each of them had to pay, we can use Python, NumPy and Matrix multiplication:
import numpy as np
NumPersons = np.array([[100, 175, 210],
[90, 160, 150],
[200, 50, 100],
[120, 0, 310]])
Price_per_100_g = np.array([2.98, 3.90, 1.99])
Price_in_Cent = np.dot(NumPersons,Price_per_100_g)
Price_in_Euro = Price_in_Cent / 100
Price_in_Euro
OUTPUT:
array([13.984, 11.907, 9.9 , 9.745])
Cross Product
Let's stop consuming delicious chocolates and come back to a more mathematical and less high-calorie topic, i.e. the cross product.
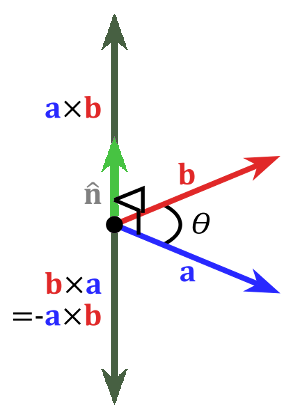
The cross product or vector product is a binary operation on two vectors in three-dimensional space. The result is a vector which is perpendicular to the vectors being multiplied and normal to the plane containing them.
The cross product of two vectors a and b is denoted by a × b.
It's defined as:
![]()
where n is a unit vector perpendicular to the plane containing a and b in the direction given by the right-hand rule.
If either of the vectors being multiplied is zero or the vectors are parallel then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors as sides. If the vectors are perpendicular the parallelogram is a rectangle and the magnitude of the product is the product of their lengths.
x = np.array([0, 0, 1])
y = np.array([0, 1, 0])
np.cross(x, y)
OUTPUT:
array([-1, 0, 0])
np.cross(y, x)
OUTPUT:
array([1, 0, 0])
